Table of Contents
その差は予測不可能
この段階で指摘しておくと、1.68インチのボールは、1.62インチのボールを単にサイズアップしただけのものではなく、またそんなことはあり得ない。もしそうだとしたら、1.62オンス(公称値)ではなく、約1.8オンスの重さになってしまう。よって単純なサイズの変更における影響は予測可能だが、実際の違いについてはより複雑な考察が必要となるはずだ。
弾性のあるゴムの糸が巻かれている中心部のコアについて考えてみよう。1.68インチのボールでは、1.62インチのボールよりも軽く、また小さくなることは間違いない。いずれにせよ、コアに巻かれる弾性糸はより多くなるので、反発力、ひいてはクラブヘッドからのスピードが予期せぬ形で違ってくる可能性がある。
さらに、1.68インチのボールでは、メーカーが糸をより強く巻く傾向にあるため、状況はさらに複雑になる。そうすれば「硬く」なるはずだが、大きいのために衝撃で変形する度合いは1.62インチのボールとお堂程度になる可能性がある。現実には、一方のボールが他方のボールより速くクラブヘッドから離れるかどうかを予測することはほぼ不可能である。
スピンについて。ボールがクラブフェースから離れる際に付与されるスピン量は、ボールの慣性モーメントに依存する。大きなボールの方が重さが中心に集中しないため、慣性モーメントは小さなボールに比べて相対的に大きくなる。スピンは、圧縮の量や接触時間など、単純に大きさだけでなく、さまざまな要因にも左右されるため、ここでも測定して確かめることが必要となる。
最後に、ボールがその飛行中にさらされる空力の影響は、単純にその大きさに左右される。大まかに言えば、その面積に比例したもの、つまり1.68インチのボールは1.62インチのボールよりも7.5%多く影響を受けると想定される。しかし少なくとも揚力については、ディンプルの形状および深さや形状が重要な要素であり、そして実際にほとんどのメーカーはそれらを調整することで異なるサイズのボールで、ほぼ同じ高さの軌道が得られるようにしている。
サイドスピンは単に揚力の働く角度の違いで発生するものであるため、スライスやフックの影響の差も、解消されないにしても小さくなることは確かである。繰り返しになるが、理論上の推測を確信にもとづいて行うことは不可能である。影響はボールのメーカーによっても異なるかも知れない。よってこれらは実際に測定をするしかない。
インパクトで発生している事実
ダンロップがドライビングマシンのテストに基づいて提供した数値は、少なくともドライバーショットにおいては、2つのサイズのボールがクラブヘッドからほとんど同じ方法で離れることを示唆している。これらのテストでは、大きなボールは小さなボールよりも約10%少ないスピン量で、約1%速く飛び出した。仰角に大きな差はなかった。
G.S.G.B.のチームは、この実験を繰り返し、ドライバーだけではなく、5番アイアンや7番アイアンのショットにも広げ、プロゴルファーにボールを打ってもらった。その結果、3つのクラブのいずれにおいても、スピード、スピン、仰角のいずれにも、ランダムな影響によって発生しうる程度を超える差は見られなかった。これらのテストの結果の一部を図26 : 3および図26 : 4に示す。

図26:3 上段の図は、プロゴルファーが双方のサイズのボールを多数打撃してテストした、7番アイアンとドライバーのボール初速である。陰になっている部分とその濃さは、放たれたボールの飛距離の分布を表している。平均値からの隔たりはロングドライブでやや大きいボールの方が大きい。
図26:4 中段は、同じく双方のボールの7番アイアンとドライバーのテストによる、ボールの回転数の分布。ここでは、ドライバーにおいては小さいボールの方がバラつきが大きく、7番アイアンでは大きいボールの方がバラつきが大きくなると言う現象が見られた。
図26:5 下段は、二つの大きさのボールを、ドライビングマシーンによって同条件で試打した場合の飛距離の分布。ここではそれぞれの平均値を比較すると、キャリーで8ヤード、ランで12ヤード小さいボールの方が飛んでいる結果になった。ただし、陰の部分が示す通り、マシーンによるテストでも飛距離にはかなりの分布が拡がっており、26:3の実験結からもわかるとおり、アベレージゴルファーはもとより、かなり優秀ながゴルファーであってもその飛距離の差を実感することは困難になる。
ある測定値が他の測定値よりも信頼性が高く一定であるという事実を考慮し、同じインパクトに対する大小のボールの反応についての研究チームの総合評価は、以下の通りである:
- 打ち出し角は同じである。
- 付与されるスピンは、おそらくほぼ同じであり、違いがあるとしても、ショットごとに得られるスピンのかなり大きなバラつきよりは大きくないことは確かである。
- 大きなボールのスピードは、伸縮性のある糸の張力と体積の増加により、小さなボールのスピードよりもごくわずかに大きくなる可能性があるものの、ここでも、違いがあるとすれば、それはショットごとのスピードの違いよりも小さい。つまり、同じクラブで同じスイングをすれば、どちらの大きさのボールもほとんど同じように飛んでいく。
飛球のバリエーション
次に、それぞれのボールの飛行特性をテストすることになった。こちらもダンロップ社から数値が提供されており、プロゴルファー(ノーマン・クイグリー氏)が打ったショットを計測した。さらに、研究チームが独自にダンロップ社のドライビングマシンを使ってのテスト、双方のボールの風洞でのテストも行い、空力に関しての基本的な情報を得ることができた。
屋外でのプロによるテストでは、ドライバー、5番アイアン、7番アイアンのいずれのクラブでも、2つのボールサイズの間に長さ(キャリー)に大きな差は見られなかった。
いっぽうで、ドライビングマシンを使ったテストでは、ロングドライブ(230ヤードから222ヤード)では約8ヤード、ショートドライブ(180ヤード→176ヤード)では4~5ヤードと、大きなボールではわずかに飛距離が減少した。大きなボールは、小さなボールよりも、より急角度に、あるいは、より少ない前進速度で着地するため、それほどランが出ない。そのため、平均的なグラウンドコンディションであれば、さらに3~5ヤードの飛距離減が発生する可能性がある。
弾道の高さは、ほぼ同じであることがわかった。意外かも知れないがこれは当然で、というのも、大きなボールのディンプルは、通常、小さなボールとほぼ同じ高さの軌道を描くように設計されているからだ。しかし、このことは、大きなボールを支持する人たちが好んで主張する、ボールをすくい上げるのではなく、ボールを前進させるようなスイングを身につけることを奨励するという主張に重大な疑問を投げかけるものである。
先に述べたように、大きなボールのディンプルを調整することによって生じる揚力の減少は、サイドスピンの影響も減少させる傾向があり、少なくともある程度は大きなボールの余分な面積による影響を補うことになる。このことも、テストでも実証された。ドライビングマシンのある設定から40ヤードほど逸れるようにフックやスライスを出すと、大小のボールでその傾向に違いは見られなかった。
また、横風の影響も調べた。これは基本的にはスピンに依存するプロセスではなく、むしろ横向きに作用する抗力である。大きいボールの揚力を小さくするディンプルは、それに応じて抗力を小さくすることは期待できず(当然、大きいボールが飛距離を失うのはそのため)、大奇異ボールは横風の影響をより強く受ける可能性がある。
この予想は、実験でも実証されましたが、理論的に予想されるよりも大きな差が見られた。平均240ヤードほどのドライブで、強い横風が吹いたとき、アメリカンサイズのボールはコースから15ヤードほど外れたのに対し、イギリスンサイズのボールは9ヤードほどしか外れなかった。
理論値では?
これらの結果の多くは、読者諸君を驚かせるものかもしれない。特に、どちらかのボールに対する説得力のありそうな意見に同意する人々にとってはなおさらである。しかしまだ驚くべきいくつかの事実が存在する。いっぽうで、飛行の違いの理由や、場合によっては、予想されるような違いがないことについて、もう少し深く考えてみる価値がある。
他の条件が同じであれば、最も単純な考察では、先ほど述べたように、揚力も抗力もボールの面積に依存し、大きなボールに働く力は小さなボールに働くものより7.5%大きいということになる。しかし、ディンプルを変更することで、メーカーはそれを微調整することができるため、その違いを正確に知るためには、風洞実験によってこの揚力と抗力を直接測定する必要がある。
その結果、アメリカのボールの抗力は、イギリスのボールよりもやはり約7.5%大きいことが確認されました。揚力も大きいが、風洞実験の制約上、実際にプレーで発生する速度よりも低い速度で観測された範囲では不規則に変動するため、どの程度なのかはわからなかった。
そこで,理論的な軌道を計算する際には,同じスピンと速度の組み合わせで,抗力と揚力の双方がアメリカサイズの方が7.5%大きいと仮定することにした.
これに基づいてコンピューターで計算された飛距離は、おおむねドライビングマシーンの結果の範囲に収まることがわかった。表 26 : 3 は,3 種類のドライブの長さについて示したものである.もちろん、ランの量は大きく変化するものであり、したがって、全体の飛距離の数値は、少し控えめに見る必要がある。とはいえ、ほとんどどのようなグラウンド条件でも、小さなボールは大きなボールより少し長くランが出ている。つまり、キャリーの差はそれなりに正確で、トータルの飛距離の差はもう少し大きく、ある平均的な地面の状態での表の数値に近いとほぼ確定できる。
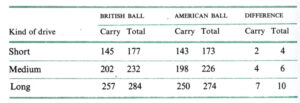
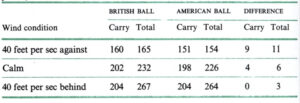
表 26 : 3 の「中間距離のドライブ」に対する向かい風と追い風の影響を計算したものが表 26 : 4 である。 表 26 : 3 と同じようにランについて留保して、全体の飛距離の 6 ヤードの差は、ドライブが強い風に向かってプレーした場合にはほぼ倍になり、風が追っている場合には半分になることが分かる。当然、この差は表 26 : 3 の「長距離ドライブ」の方が大きく,「短距離ドライブ」の方が小さくなる。
計算の結果、少し意外だったのは、揚力が 7.5 % も異なると想定したにもかかわらず、計算された軌道の高さは、大きなボールが小さなボールより 5 % だけ大きく (60 フィートで 3 フィート)、飛行時間は 2.5% だけ大きくなったことだ。先に述べたように、実際には揚力は7.5%よりも大きいとは考えられないので、このわずかな差も実情よりも大きいものになっていると考えられる。ちなみに、1.68インチのボールの飛行時間がわずかに長いということは、ドライブにおけるキャリーの減少が、抗力の増加にもかかわらず意外に小さいということを物語っている。飛行時間が2.5%延びると、大きなボールの抗力によるキャリーの計算上の減少分から、およそ5ヤードが「取り戻される」ことになるのだ。