Table of Contents
第二十三章 ゴルフの弾道学:スピンと飛行はどのように起きるのか
ドライバーのフルショットにおいて、クラブヘッドが時速100マイルでボールに飛び込む場合、ボールが空中に飛行を始める、また飛行中にスピンがかかるという、主に二つのモーションがボールには与えられる。
この二つのモーションのうち、ボールにスピンをかける方法はより複雑なメカニズムであるため、ここではまずボールを空中に飛ばすにあたって最も単純な方法、つまりロフトのないクラブでスクエアにインパクトをする際に何が起きているのかをまず考えてみたい。こうした状況は実際のゴルフのショットにおいては非現実的だが、大気中を飛行するボールの速度の源が何であるのかを、正確さを失うことなくシンプルに突き止めることができる。第20章で述べた通り、ボールに与えられる「前に飛ぶ」スピードのみについて考慮する場合、ドライバーをロフトのない者として考えるのは非常に理にかなっているのだ。
ゴルフのストロークは衝突である
最初に明確にしておきたいことは、ボールはクラブヘッドによって、いかなる方法においても「投げられている」わけではないということだ。それとは逆に、直接的な衝突によってボールは飛行状態に投入されるのである。
ここで起きている衝突の、典型的な三つのステージを図にしたものが23:1の図である。

23:1 ドライバーショットにおける三つのステージ。上から、ファーストコンタクトの直後、インパクト中にボールが変形する時点、ボールがクラブフェースから離れた直後を表している。
ステージ1と2において、クラブヘッドの運動エネルギーの一部はボールを変形させることに使用され、ボールの内部で弾性エネルギーとして蓄積される。このボールが変形している状態では、ボールはクラブフェースと全く同じ速度で動いていなければならないが、つまりその一瞬において、ボールとクラブヘッドは統合された一つの質量を形成する。
この一瞬にボールとクラブヘッドが動く速度は、インパクト前の相対重量と速度によって決定される。このロフトがないドライバーの単純なモデルでは、時速100マイルで動く重さ7オンスのクラブヘッドは、衝突によって時速19マイル速度が減少し、つまりクラブヘッドとボールの双方が時速81マイルで動いている。
ステージ2の後にボールの弾性エネルギーが開放され、元の球体に復元される際、ボールはクラブフェースから「ボール自身を押し出す」ことになり、同時にクラブヘッドをわずかに後方に押し戻す。その際にボールが、減速したクラブヘッドよりも大きな余剰速度を得られるのは、ボールの質量がクラブヘッドよりも軽いからという単純な理由によるものである。
よって図のステージ3に移行する時点で、ボールはクラブフェースから完全に離れ、その速度はさらに時速54マイル増加し、クラブヘッドの速度はさらに12マイル減少する。よって最終的な双方の速度は、ボールの初速が時速135マイル、クラブヘッドの速度が69マイルになる。
重要な要素: 反発(Bounce)のエネルギー
時速 100 マイルの衝突から生じる最終速度の正確な測定値は、基本的にはクラブヘッドの元の運動エネルギー (キネティックエナジー) のどの程度の割合で失われるかに大きく依存している。クラブヘッドとボールの衝突の際は常に、この運動エネルギーの一部が圧縮エネルギー(弾性エネルギー)に転換される過程でロスが発生し、インパクトが終了する時点で再び運動エネルギーに開放されるということが起きている。
従いゴルフでは、クラブフェースとの「完全弾性衝突」になるほどボールが飛ぶことは起きえない。もしそのようなインパクトが可能であるとすれば、その違いはクラブヘッド操作におけるステージ2に違いが発生するはずであり、ステージ1ではない。
ステージ1の現象に影響するのは質量と速度のみである。仮に7オンスのクラブヘッドで、ボールと同じ1.62オンスの粘土のような物体を時速100マイルのヘッドスピードで打撃した場合、クラブヘッドと粘土の双方はステージ2において時速81マイルに到達するが、(粘土がクラブフェースに貼り付いたままになってしまう限り)、その後の双方の速度には変化は起きない。
全く同じ条件のステージ1の効果を、完全弾性衝突のインパクトに応用した場合を考えてみる。この場合、最終的な速度は、クラブヘッドの場合で遅くなり、ボールの場合で速くなるが、これは双方が反発する反応によってエネルギーの総量が増加するからである。
双方の例を示したものが図23:2である。




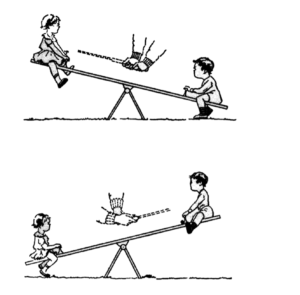
23:2 弾性のないインパクトと、完全弾性衝突のインパクトの比較。上図では三つのステージのインパクト前後を、粘土のようなゴルフボール(反発係数ゼロ)を打撃する場合を表している。下図では同様のステージを完全弾性衝突(反発係数=1)の場合を想定して表現している。
ここまでの説明で、ドライバーの飛距離はクラブフェースとボールの衝突の際の弾性が、いかに重要な意味を持つかがお分かりいただけたと思う。そしてもちろんこの弾性は、クラブの挙動よりもボール挙動の弾性により大きく影響されるが、それはクラブフェースはボールよりも遥かに硬いため、クラブヘッドの実質的な変形はわずかでありそこで生まれるエネルギーのロスもほとんど発生しないからである。
バウンス=「反発係数」
弾性の異なる状況かで、与えられる最終的な速度がどのように変化するのかについては、興味があれば巻末の付録Iの実際の計算に用いる方程式を参照されたい。結局のところ、ボールが飛び立つ速度は、クラブヘッドがボールを打撃する際のヘッドスピードのX倍であり、Xの大きさはクラブヘッドとボールの相対的重量と、「反発係数(Coefficient of Restitution)」呼ばれる数値によって決定されるが、これはある衝突がどの程度「完全弾性衝突」に近づくのかを数学的に示す方法でしかない(注:完全弾性衝突の場合、反発係数は「1」になる)。
反発係数を極限まで高めるということは、現実的なビジネスとしてゴルフボールの製造を行う観点からすればあまり有用なものではない。クラブでインパクトをした瞬間にボールが粉々になってしまうことは避けなければならず、つまりボールはインパクトでの内部応力を妥当な範囲内に維持するのに十分な程度まで弾性的に変形する必要がある。
例えば、ガラスのビー玉を石の床に落とした場合、ゴルフボールよりも反発係数が高いためより鋭く跳ね返る。しかしこれをゴルフクラブで打とうとしても粉々になるだけなのだ。
なぜボールはクラブによって変形しなければならいのか
インパクト時に物質に発生する内部応力は、その物質の変形に対抗する量に反比例する。ごく大まかに言えば、変形が半分になれば、素材で生成される内部応力は二倍になる。ビー玉のような物質の場合、ゴルフボールと比較して10,000分の1程度しか変形しない。もしこのような物質が強い打撃にさらされた場合、強大な内部応力が発生するため、ビー玉は粉々になってしまう。
従いゴルフボールにはクラブからの強打に対して、文字通り「弾力性」が必要であり、それによって打撃の際に生じる内部応力が、ボールを破壊してしまわない範囲に維持する必要がある。また同時にインパクト後に、強力にもとの形状を復元するパフォーマンスも非常に高いレベルで要求される。
ボールのメーカーがこれをどのように達成しようとしているのかについては、ここでは詳しく説明する必要はないだろう(第26章を参照のこと)。しかし本章の写真から、ゴルフボールがどれほどクラブフェースに対して変形し、また急激に元の形状を復元しているのかを理解できるはずだ。
また前述の通り、スクエアインパクトにおける理論上の最大値である時速162マイルに対して、一般的に達成されている135マイルという数値を見ても、メーカーがいかにこの二つの本質的品質を達成することに成功しているかを見て取ることができる。
クラブヘッドの要因
この問題については第32章で詳細に説明を行う。それまで読者諸君は、第1章の「重量」という見出しの段落をもう一度よく見ておいてほしいのだが、要はクラブヘッド重量が重いほどボール初速も速くなり、遠くに飛ぶということである。
これは事実だが、あくまでそのより重量のあるクラブを同じ速度でスイングできればという条件付きであり、現実にはクラブヘッドの重量とスイングスピードは、一般的な7オンスあたりの重量で双方の影響が良いバランスとなる結果になっている。実際に標準的な7オンスからプラスマイナス3オンスの重量帯で実験を行っても、飛距離への影響は驚くほどわずかであった。なぜこのようなことが起きるのかは第32章で取り上げる。