今週は明日がラウンドで明後日は岩手の安比高原に森美穂さんの応援(コニカミノルタ)いくつもりだよー
Table of Contents
2-E 運動量保存の法則
直線的に衝突をした物体は、衝突する前の速度を超えて物体が離れることは不可能なのじゃ
つまりゴルフのストロークで、ボールにぶつかったヘッドは、必ずぶつかる前よりその速度が下がるということだねー
衝突の後のヘッドスピードと衝突の前のヘッドスピードの割合は、ボールの弾力性によっても左右されるが、これは反発係数(Coefficient of Restitution)と呼ばれており、良いボールを使った場合これは約80%ほどになるが、ヘッドスピードが早くなると70%まで低下する
今のルールでは、反発係数の上限は0.830までって決まってるみたいだけど、意外と爺の時代とそんなには変わってないと言うことだよねー
今の方が昔よりドライバーの平均飛距離が伸びてることは間違いないとは思うんだけど、それって実はシャフト(の材質や長尺化)とボールの進化による部分が大きいのかもしれないねー
当然のことながら、コンプレッションの漏れ(2-C-0)が発生した場合、このパーセンテージはさらに減少することになるのじゃ
この事実が意味するところは、いかに幾何学的に正しい位置関係でインパクトを迎えるとしても、ボールがクラブフェースから離れる際のスピードは、クラブヘッドがボールに近づいてきたときのスピードの80%以上にはならないということじゃ
よってこの条件下でおおざっぱに計算をすると、クラブヘッドが時速100マイル(秒速でへッドピード換算すると44.44m/s)でボールに近づいてきたとすると、ボールがフェースから離れるときには80マイル(同35.55m/s)に減速し、ボールの初速は70マイルほど(同31.11m/s)、つまりボールに近づいているときのヘッドのスピードのおよそ70%ほどになるということじゃ
この条件下ではボールは時速150マイル(同約67m/s)に達することとなる
唐突にこの数字が出てくるんだけど、仮によくいうミート率ってことだと、ヘッドのアプローチスピードが一般的な「ヘッドスピード」ってことだとすると、ヘッドスピード100マイルに対してボールスピードが150マイルってことは、ミート率1.50になるんだけど、まぁ完璧にミートしてロフトがゼロならあり得るのかもしれないねー
同じ条件下で、もしボールとフェースが離れる際のヘッドのスピードが40マイルであるならば、ボールは110マイルにしかならないということじゃ
ん?ボールがフェースと離れるときに40マイルなら、アプローチスピードは50マイルで、ミート率1.50でも75マイルにしかならないと思うんだけど、この位の速度だとミート率は上がるって事なのかな
どっちにしろこのくらいのヘッドスピードって短いショットだと思うし、当然短い番手だとパワーがロフトでバックスピンに転換される割合が増えるからあんまり現実的ではない数字だと思うから無視して先に進むよー
重要なことは、ボールが取得出来る初速はクラブヘッドのアプローチスピードの70%になるということであり、つまり飛距離のためにはヘッドスピードが必要であるということと、ボール初速はボールとクラブフェースが離れる際のクラブヘッドの100%のスピードになると言うことは、クラブヘッドを減速させる割合をなるべく少なくするための抵抗が必要ということじゃ
理論上インパクトにおけるヘッドの減速がゼロであるということは、いかなるクラブ、あるいはいかなるヘッドスピードのストロークにおいても、ボール速度を最大にすることを可能にするものじゃ
現実的にはクラブヘッド軌道にかかる遠心力によって得られるスピードと、ヘッド加速によってストレスがかかることでクラブシャフトが硬くなった状態が、インパクトの間じゅう継続した状態で保持出来ることが(弱いストロークであれ、強いストロークであれ)、ヘッドの減速に対抗する手段となるのじゃ
感覚的にはクラブヘッドが「しなった状態から戻る」感覚が「とても重く」感じるようにクラブを扱うということで、実際のボールは既に遠くに飛んで行ってしまっているとしても、インパクトが継続しておるかのようなつもりでフィニッシュまで迎える事じゃ(7-11も参照のこと)
TGMでずっと言ってることだけど、一般的なヘボゴルファーの場合は切り返しで「ふんっ!」ってチカラ入って、インパクトまでラグを継続出来ないんだけど、ラグはインパクトの後までずっと継続させないとここで言ってる「クラブヘッドの減速」が大きくなっちゃうと
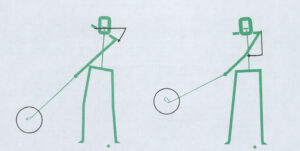
pp#3にどのくらいの割合でプレッシャーがかかっているかについて言及しているwww.GolfLagTips.comさんというところの図をお借りすると
一般的ヘボゴルファーの場合

PGAツアープレイヤーの場合

インパクトにかけて、長く一定のラグを感じながら、ボールが絶対飛んでいった後までそれを継続するってことだよねー
インパクトにおけるバワーの分散および、ボールが離れていく際のベクトル(2-C-1/2/3)は、常にアタックアングルとラインオブコンプレッションの総和に等しく、結果その合力の方向にリザルタントベクターを生じることとなるが、それは結局フェース面とリーディングエッジに対してスクエアなものとなり、ラインオブフライトの方向は上記のベクトルと平行であるスイートスポットのラインであるセンターライン上になるのじゃ
もしラインオブコンプレッションがセンターライン上にないとすると、発生するバックスピンには傾きが加えられることとなるのじゃ(2-B)
この傾きは、上記の要因がインパクトにおいてどの程度ズレたかに相応したものとなるのじゃが、これを利用してボールの方向を変えることはもちろん可能じゃ(2-D、7-2)
TGM的な飛球法則まとめ

上の図は、下のアイアンがボールコンタクト時のフェース向きで、上の図がボールセパレーション時のフェース向きになるよー
上の図のようにクラブヘッドの移動アークと、スイートスポットの移動アークが完全に同一円心状、言い換えれば平行であるならば、どこでボールにコンタクトして、どこでボールが離れようが、必ずボールはフェースから離れたときのフェースおよびリーディングエッジに直角な方向に飛び出すのであり、この場合のみバックスピンの回転軸に傾きが発生しない(純粋にバックスピンのみになる)ってことみたいよー
ちなみに上の図って、スインガーのヒンジングと同じ状況だよー
でもって上の図の赤線の平行関係が崩れるような操作をした場合、たとえばレイバックな打ち方でクラブが閉じた状態で入ってきて開いて抜けるような感じになると、たぶん左の赤線はもっと左側に傾くことになるけど、その場合はボールはとりあえずフェースから離れるときのフェース方向に飛び出すけど、バックスピンは右に傾くから右にスライスするチカラが発生するよーと、フックはその逆ね
で、どんだけ曲がるかは、上の二本の赤線が平行な状態からどんだけ崩れる方向にフェース操作をしたかの度合いによるよって事みたい
でこれが面白いなと思うのは、Dプレーンの説明とだいぶ違うところで、Dプレーンではクラブヘッド軌道とインパクト時のフェース向きのズレで曲がりが発生するって言うんだけど、TGMの理屈ではクラブヘッド軌道(上の図の外側の円)とボールセパレーション時のフェース向き(上の図の上の方のアイアンの状態)は、全部同じでもストレートもスライスもフックも打てるってことになるよねー
でもってコンタクト時のフェース向き(下のアイアン)をベースに考えてDプレーンの理論を当てはめると、今度は曲がる向きが逆になっちゃうのね
つまりDプレーンはインパクトを「点」でとらえていて(かつその「点」がどこなのか定義されてないんだけど)その瞬間のフェース向きとラインオブコンプレッションでボールの曲がりを説明しようとしてるんだけど、おいらが客観的に見てもそれだと説明し切れない現象があるような気がするんだけどもー
まぁそもそもどっちの理屈も全部スイートスポットに当たったらって仮定での話だしねー
良いスイング軌道と良いヒンジアクションを経験的に作っていくということしか現実的でないと思うよー
またボールの止まり方について言えば、飛球がグリーンにヒットした際に発生する摩擦によってもベンチュリー効果(マグヌス効果ね)のアクション発生するのであり、ボールマークが深ければ深いほど(あるいは「めり込む」ということもあるが)より大きな摩擦が発生するのであり、これらの効果によってボールがどの程度「止まる(Bite)」のかが決定されるのじゃ
一方ゴルフボールの回転は、(ボウリングのボールのように)一定方向へのスピンを維持しながら「転がる」と言うことが出来るほどの角運動量を持たないため、直線的な運動に負けてしまうので、スピンによってカーブさせるパットを打つ事は難しいのじゃ
やろうとも思わないけどねー
やっとこの面倒くせーパート終わったよー
こっから先ももちろん面倒くさいけどねー